Amélioration des indices d'autocorrélation spatiale, des méthodes d'estimation et de modélisation spatiale par standardisation sur la distance
ISPRS Int. J. Geo-Inf. 2019, 8(4), 199; https://doi.org/10.3390/ijgi8040199 - 24 Avril 2019
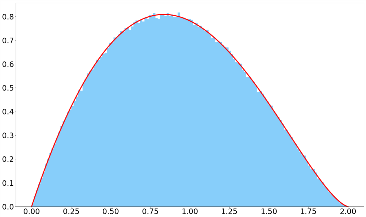
Résumé Etant donné un ensemble de points dans un espace de dimension supérieure
à 1, la distribution statistique du nombre de couples de points en fonction de
leur distance n'est pas constante. Cette distribution n'est pas prise en compte
dans un grand nombre de méthodes classiques utilisées en analyse spatiale et
basées sur des moyennes, comme les indices d'autocorrélation spatiale, les
méthodes d'interpolation par noyau ou les méthodes de modélisation spatiale
(autorégressive ou géographiquement pondérée). Cette distribution a un impact
direct sur les calculs et les résultats des indices et des estimations et
en ne tenant pas compte de cette distribution des distances, les calculs
d'analyse spatiale peuvent être biaisés. Dans cet article, nous introduisons
une "standardisation spatiale", qui corrige et ajuste les calculs par
rapport à la distribution des couples de points en fonction de leurs distances.
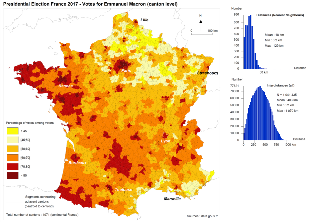
A titre d'exemple, nous appliquons cette correction au calcul des indices
d'autocorrélation spatiale (indices de Moran et de Geary) et au calcul de
surface de tendance (par interpolation spatiale par noyau) sur les résultats de
l'élection présidentielle française de 2017.
ISPRS Int. J. Geo-Inf. 2019, 8(4), 199; https://doi.org/10.3390/ijgi8040199 - 24 April 2019
Abstract
In a point set in dimension superior to 1, the statistical distribution of the number of pairs of points as a function of distance between the points of the pair is not uniform. This distribution is not considered in a large number of classic methods based on spatially weighted means used in spatial analysis, such as spatial autocorrelation indices, kernel interpolation methods, or spatial modeling methods (autoregressive, or geographically weighted). It has a direct impact on the calculations and the results of indices and estimations, and by not taking into account this distribution of the distances, spatial analysis calculations can be biased. In this article, we introduce a "spatial standardization", which corrects and adjusts the calculations with respect to the distribution of point pairs distances. As an example, we apply this correction to the calculation of spatial autocorrelation indices (Moran and Geary indices) and to trend surface calculation (by spatial kernel interpolation) on the results of the 2017 French presidential election. Full article